32_Logistic_Regression_로지스틱회귀

공부 시간, 과외 시간 성적 사이의 관계는 좌표로
나타낼 때 형태가 직선으로 해결되는 선형 회귀를
사용하기에 적합했었다.
공부 시간에 따른 점수가 아닌 합격 여부로 발표되는
시험이 있을 경우 직선으로 해결하기에는 적합하지
못하는 문제가 발생한다. 이럴 때 사용하는 로지스틱
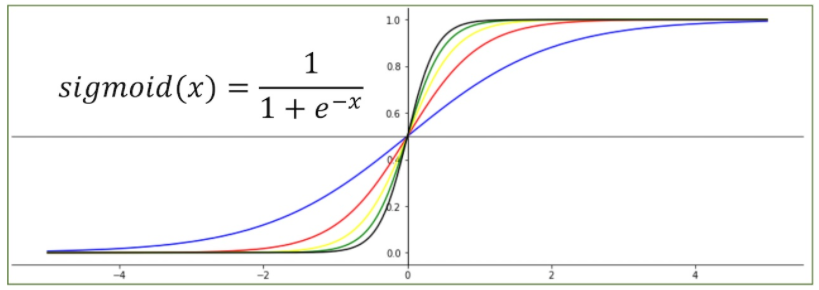
회귀는 참과 거짓 중에 하나를 내놓는 과정으로 참과
거짓을 구분한 ‘S’자를 눕혀놓은 형태의 선을 그어주는
작업이다.
참조 사이트
http://taewan.kim/post/sigmoid_diff/
https://devlog.jwgo.kr/2018/04/16/sigmoid-graph-according-to-slope-change/

from IPython.display import Image
Image('./sigmoid.png', width ='800')

import warnings 
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()

#공부 시간(x), 합격 여부(y) =>[공부 시간, 합격 여부]
data=[[2,0],[4,0],[6,0],[8,1],[10,1],[12,1],[14,1]]
xData=[i[0] for i in data] #공부한 시간
yData=[i[1] for i in data] #합격여부
print(xData)
print(yData)

[2, 4, 6, 8, 10, 12, 14]
[0, 0, 0, 1, 1, 1, 1]

#기울기(a), y절편(b)값을 랜덤하게 정한다.
#random_normal()함수는 tensorflow에서 정규
#분포를 따르는 난수를 발생시킨다.
a = tf.Variable(tf.random_normal([1], dtype=tf.float64))
b = tf.Variable(tf.random_normal([1], dtype=tf.float64))
sess = tf.Session()
sess.run(tf.global_variables_initializer())
print('a={},b={}'.format(sess.run(a),sess.run(b)))

a=[-0.60326647],b=[0.72928339]

#np.e : 넘파이에 지수값(2.718)을 의미하는 상수
#print(np.e)
y = 1/(1+np.e**-(a*xData+b))

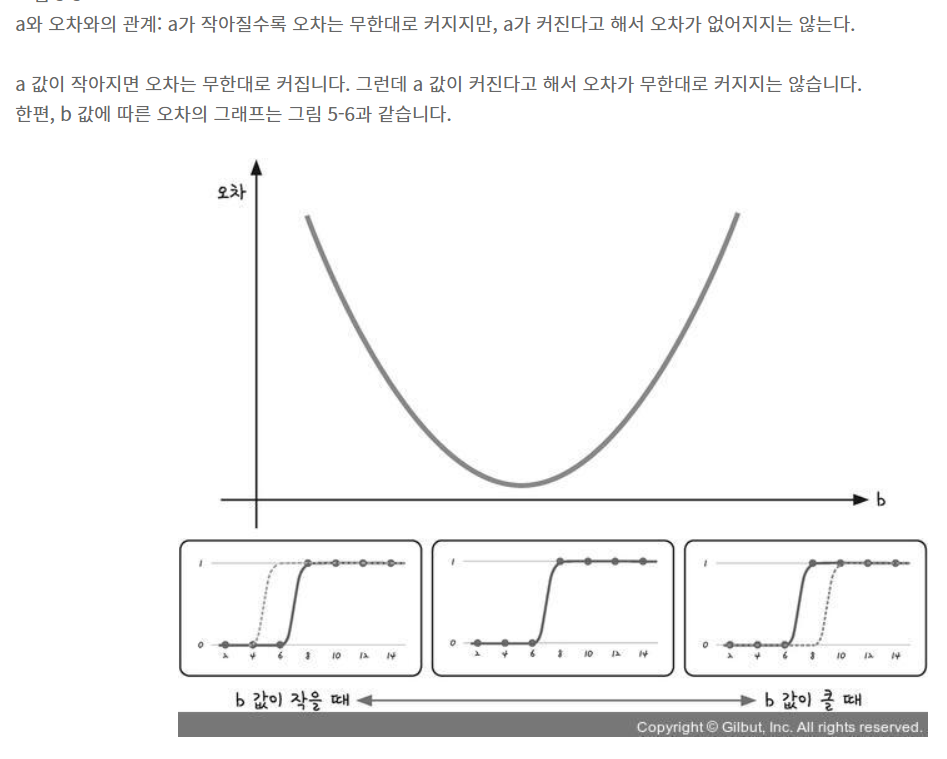
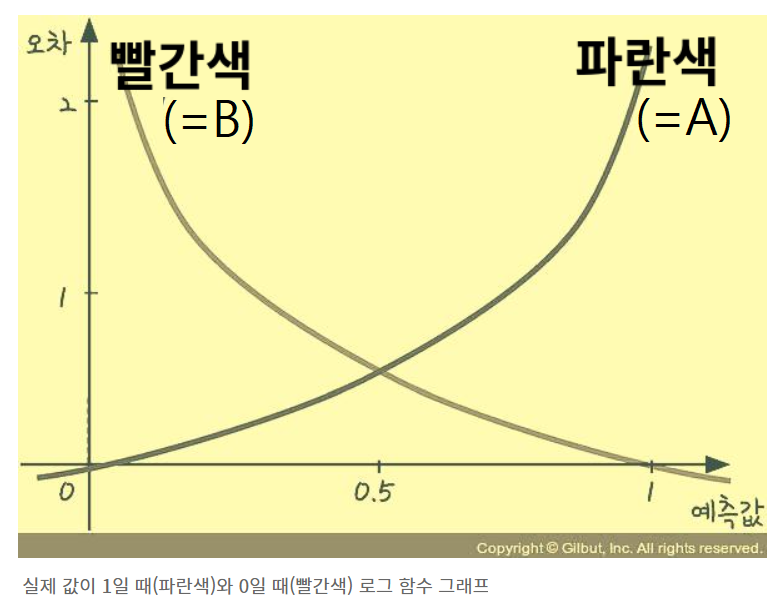
시그모이드 방정식의 오차를 계산하는 함수를 만든다.
시그모이드 함수의 특성은 예측값(y)이 항상 0아니면
1이라는 것이다.

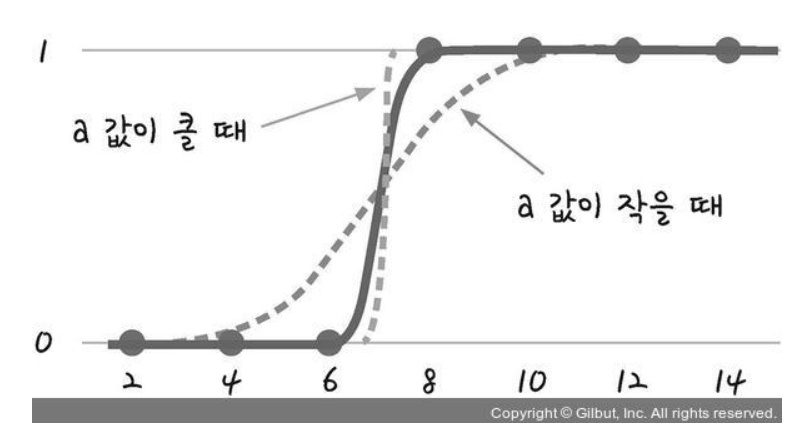
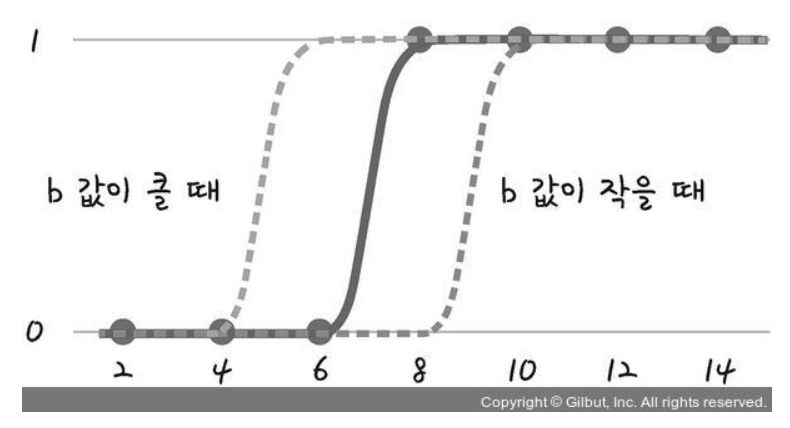
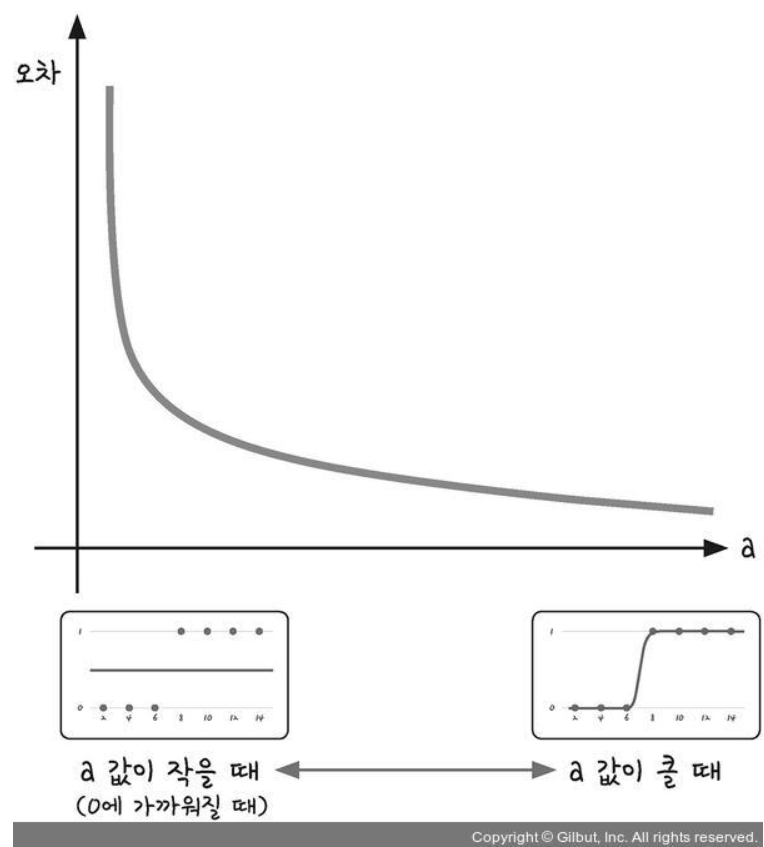
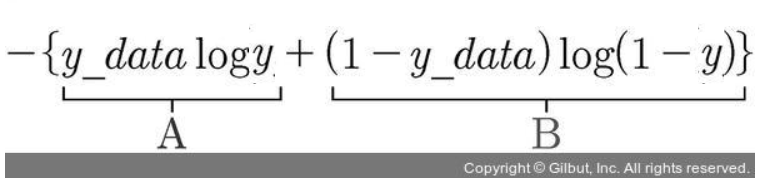
https://ang-love-chang.tistory.com/25

loss = -tf.reduce_mean(np.array(yData) * tf.log(y) +(1-np.array(yData)) * tf.log(1-y))

오차를 최소로 하는 값을 찾는다.

gradient_descent = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

학습시킨다.

sess = tf.Session()
sess.run(tf.global_variables_initializer())

for i in range(320001):
    sess.run(gradient_descent)
    if i % 20000 ==0:
        print('Epock:{0:4d}, loss:{1:10.6f}, 기울기:{2:10.6f}, y절편:{3:10.6f}'
             .format(i, sess.run(loss), sess.run(a)[0], sess.run(b)[0]))

Epock:   0, loss:  1.877932, 기울기: -0.203560, y절편: -0.865261
Epock:20000, loss:  0.021687, 기울기:  2.557518, y절편:-17.748803
Epock:40000, loss:  0.011839, 기울기:  3.175019, y절편:-22.077760
Epock:60000, loss:  0.008110, 기울기:  3.558666, y절편:-24.765468
Epock:80000, loss:  0.006157, 기울기:  3.837153, y절편:-26.715956
Epock:100000, loss:  0.004958, 기울기:  4.055662, y절편:-28.246170
Epock:120000, loss:  0.004148, 기울기:  4.235398, y절편:-29.504755
Epock:140000, loss:  0.003564, 기울기:  4.388015, y절편:-30.573376
Epock:160000, loss:  0.003124, 기울기:  4.520602, y절편:-31.501713
Epock:180000, loss:  0.002780, 기울기:  4.637793, y절편:-32.322229
Epock:200000, loss:  0.002504, 기울기:  4.742783, y절편:-33.057301
Epock:220000, loss:  0.002278, 기울기:  4.837867, y절편:-33.723002
Epock:240000, loss:  0.002089, 기울기:  4.924748, y절편:-34.331265
Epock:260000, loss:  0.001929, 기울기:  5.004726, y절편:-34.891193
Epock:280000, loss:  0.001791, 기울기:  5.078815, y절편:-35.409884
Epock:300000, loss:  0.001672, 기울기:  5.147820, y절편:-35.892983
Epock:320000, loss:  0.001568, 기울기:  5.212394, y절편:-36.345051