33_Multi_Logistic_Regression_다중로지스틱회귀

import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import tensorflow.compat.v1 as tf
tf.disable_v2_behavior()

WARNING:tensorflow:From c:\python\lib\site-packages\tensorflow\python\compat\v2_compat.py:101: disable_resource_variables (from tensorflow.python.ops.variable_scope) is deprecated and will be removed in a future version.
Instructions for updating:
non-resource variables are not supported in the long term

학습 데이터를 만든다.

# xData => [공부 시간, 과외 시간]
temp = [[2, 3], [4, 3], [6, 4], [8, 6], [10, 7], [12, 8], [14, 9]]
print(type(temp))
print(temp)

# array() 함수로 파이썬 리스트를 넘파이 배열로 만든다.
xData = np.array(temp)
print(type(xData))
print(xData)

<class 'list'>
[[2, 3], [4, 3], [6, 4], [8, 6], [10, 7], [12, 8], [14, 9]]
<class 'numpy.ndarray'>
[[ 2  3]
 [ 4  3]
 [ 6  4]
 [ 8  6]
 [10  7]
 [12  8]
 [14  9]]

from IPython.display import Image
Image('./reshape.png', width ='800')

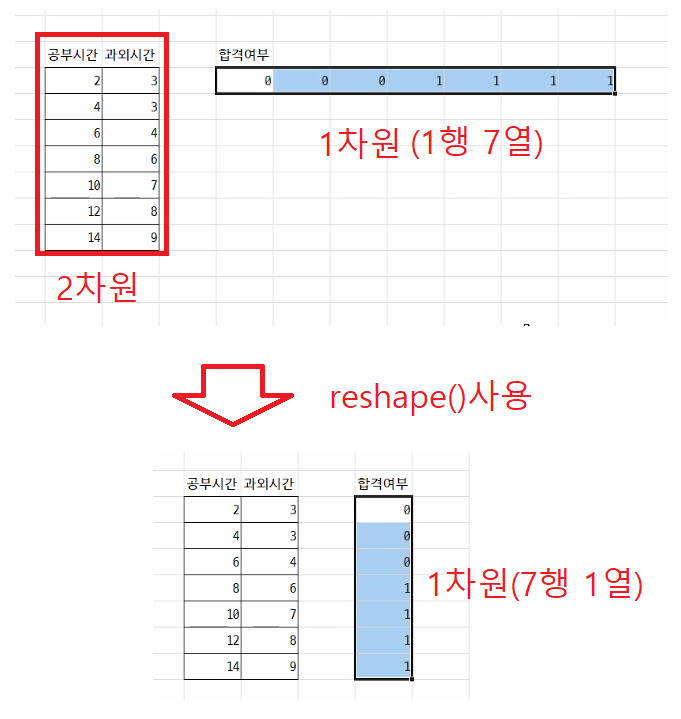
# yData => [합격 여부] => 실제값, 0: 불합격, 1: 합격
temp = [0, 0, 0, 1, 1, 1, 1]
print(type(temp))
print(temp)

# yData = np.array(temp) # 1행 7열인 1차원 배열
# print(type(yData))
# print(yData)
# print(yData.ndim)

# reshape() 함수로 1행 7열인 1차원 넘파이 배열을 7행 1열인 2차원 넘파이 배열로 변환한다.
yData = np.array(temp).reshape(7, 1)
print(type(yData))
print(yData)
print(yData.ndim)

<class 'list'>
[0, 0, 0, 1, 1, 1, 1]
<class 'numpy.ndarray'>
[[0]
 [0]
 [0]
 [1]
 [1]
 [1]
 [1]]
2

xData와 yData를 저장할 placeholder를 만든다.

# placeholder에 넘파이 배열을 대입하는 경우 shape 속성을 이용해서 대입되는 넘파이 배열의 차원을 지정해야 한다.
# [None, 2] => placeholder에 대입되는 넘파이 배열은 행의 개수는 몇개라도 상관없고 열의 개수는 무조건 2개이다.
X = tf.placeholder(dtype=tf.float32, shape=[None, 2]) # xData가 대입될 placeholder
Y = tf.placeholder(dtype=tf.float32, shape=[None, 1]) # yData가 대입될 placeholder

기울기(가중치) a와 y절편(바이어스) b를 임의로 정한다.

from IPython.display import Image
Image('./innerproduct.png', width ='800')

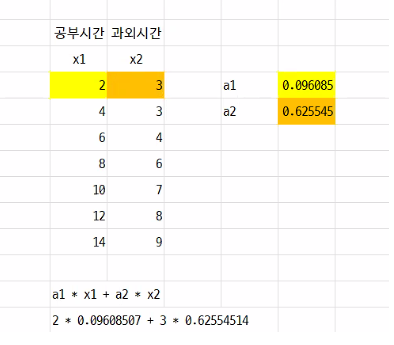
a = tf.Variable(tf.random_uniform([2, 1]), tf.float32) # 난수를 2행 1열로 만든다. => 행렬의 내적(곱)을 이용해 처리한다.
b = tf.Variable(tf.random_uniform([1]), tf.float32)

sess = tf.Session()
sess.run(tf.global_variables_initializer())
print('a = {}'.format(sess.run(a)))
print('b = {}'.format(sess.run(b)))
print('a1 = {}, a2 = {}, b = {}'.format(sess.run(a)[0], sess.run(a)[1], sess.run(b)))

a = [[0.60752  ]
 [0.9765004]]
b = [0.55916774]
a1 = [0.60752], a2 = [0.9765004], b = [0.55916774]

시그모이드 방정식, 오차 함수, 경사 하강

# sigmoid() 함수로 tensorflow에서 시그모이드 방정식을 계산한다.
# matmul() 함수로 tensorflow에서 행렬의 내적(곱)을 계산한다.
y = tf.sigmoid(tf.matmul(X, a) + b)
loss = -tf.reduce_mean(Y * tf.log(y) + (1 - Y) * tf.log(1 - y))
gradient_descent = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

sigmoid() 함수의 실행 결과(y)가 0.5 이상이면 1을 0.5 미만이면 0을 리턴시킨다.

sess = tf.Session()
# cast(캐스팅할 데이터, dtype=캐스팅할 데이터 타입) 함수로 tensorflow에서 형변환을 실행한다.
# predicted = tf.cast(tf.constant([1.9, 2.1]), dtype=tf.int32)
# print(sess.run(predicted)) # [1 2]

# case() 함수는 캐스팅할 데이터가 boolean 타입이면 True는 1로 False는 0으로 캐스팅 한다.
predicted = tf.cast(0.4 >= 0.5, dtype=tf.int32)
print(sess.run(predicted))
predicted = tf.cast(0.5 >= 0.5, dtype=tf.int32)
print(sess.run(predicted))

0
1

sigmoid() 함수를 실행한 예측값을 계산한다.

predicted = tf.cast(y >= 0.5, dtype=tf.float32) # 예측값, sigmoid() 함수를 실행한 결과(y)를 0 또는 1로 변환한다.
# sigmoid() 함수를 실행해서 얻은 예측값(predicted)이 실제값(Y)과 일치하는 정도(정확도, accuracy)를 계산한다.
# equal()는 tensorflow에서 인수로 지정된 값이 같으면 True, 다르면 False를 리턴한다.
# equal() 함수로 예측값(predicted)과 실제값(Y)이 같은가 비교한 후 리턴되는 True 또는 False를 1 또는 0으로 캐스팅하고 시행된
# 전체 결과의 평균을 계산한다.
accuracy = tf.reduce_mean(tf.cast(tf.equal(predicted, Y), dtype=tf.float32)) # 정확도

학습시킨다.

sess = tf.Session()
sess.run(tf.global_variables_initializer())

for i in range(3001):
    # sess.run([기울기, y절편, 오차함수, 경사하강], feed_dict={X: 입력 데이터, Y: 입력 데이터에 따른 실제값})
    # 연산을 하긴 하는데 결과를 사용하지 않을 실행 결과를 기억하는 변수는 '_'로 사용한다.
    a_, b_, loss_, _ = sess.run([a, b, loss, gradient_descent], feed_dict={X: xData, Y: yData})
    if i % 300 == 0:
        # Epoch: 학습 횟수, a1: 공부 시간 기울기, a2: 과외 시간 기울기, b: y절편, loss: 오차 함수
        # print('Epoch: %4d, a1: %9.5f, a2: %9.5f, b: %9.5f, loss: %9.5f' % (i, a_[0], a_[1], b_, loss_))
        print('Epoch: {0:4d}, a1: {1:9.5f}, a2: {2:9.5f}, b: {3:9.5f}, loss: {4:9.5f}'.format(i, a_[0][0], a_[1][0], b_[0],
                                                                                              loss_))

Epoch:    0, a1:   0.09320, a2:   0.30491, b:   0.23498, loss:   1.21000
Epoch:  300, a1:   0.77430, a2:  -0.47258, b:  -2.56048, loss:   0.25885
Epoch:  600, a1:   0.78320, a2:  -0.21881, b:  -3.99781, loss:   0.18666
Epoch:  900, a1:   0.70171, a2:   0.09328, b:  -5.04171, loss:   0.14660
Epoch: 1200, a1:   0.60485, a2:   0.38777, b:  -5.86999, loss:   0.12043
Epoch: 1500, a1:   0.51117, a2:   0.65186, b:  -6.55845, loss:   0.10195
Epoch: 1800, a1:   0.42572, a2:   0.88586, b:  -7.14814, loss:   0.08826
Epoch: 2100, a1:   0.34933, a2:   1.09320, b:  -7.66412, loss:   0.07774
Epoch: 2400, a1:   0.28144, a2:   1.27775, b:  -8.12293, loss:   0.06942
Epoch: 2700, a1:   0.22105, a2:   1.44302, b:  -8.53607, loss:   0.06269
Epoch: 3000, a1:   0.16717, a2:   1.59202, b:  -8.91188, loss:   0.05714

# 테스트 데이터를 만든다.
# new_x = np.array([6, 5]) # 테스트 데이터가 1차원 넘파이 배열이기 때문에 행렬의 곱셈 연산이 실행되지 않는다.
# print(new_x) # [6 5] => 1차원
# print(new_x.shape) # (2,) => 1차원
# print(new_x.ndim) # 1 => 1차원

# reshape() 함수로 테스트 데이터를 1행 2열인 2차원 넘파이 배열로 변환해야 행렬의 곱셈 연산이 제대로 실행된다.
new_x = np.array([6, 5]).reshape(1, 2)
# print(new_x) # [[6 5]] => 2차원
# print(new_x.shape) # (1, 2) => 2차원
# print(new_x.ndim) # 2 => 2차원

# sigmoid() 함수의 연산 결과에 테스트 데이터를 대입해서 연산한다.
result, new_y = sess.run([predicted, y], feed_dict={X: new_x})
# print('공부 시간: %d, 과외 시간: %d' % (new_x[:, 0], new_x[:, 1]))
# print('공부 시간: {}, 과외 시간: {}'.format(new_x[:, 0][0], new_x[:, 1][0]))
print('공부 시간: {}, 과외 시간: {}'.format(new_x[0, 0], new_x[0, 1]))
# print('합격 여부: %s, 합격 확률: %6.2f%%' % ('합격' if result == 1 else '불합격', new_y * 100))
print('합격 여부: {0:s}, 합격 확률: {1:6.2f}%'.format('합격' if result == 1 else '불합격', new_y[0][0] * 100))

공부 시간: 6, 과외 시간: 5
합격 여부: 합격, 합격 확률:  51.28%

# 공부는 1시간도 안하고 과외 수업만 0 ~ 10 시간을 받았을 경우 합격 여부와 합격 확률을 계산한다.
for i in range(11):
    new_x = np.array([0, i]).reshape(1, 2)
    result, new_y = sess.run([predicted, y], feed_dict={X: new_x})
    print('공부 시간: {0:2d}, 과외 시간: {1:2d}'.format(new_x[0, 0], new_x[0, 1]), end=' ')
    print('합격 여부: {0:s}, 합격 확률: {1:6.2f}%'.format('  합격' if result == 1 else '불합격', new_y[0][0] * 100))

공부 시간:  0, 과외 시간:  0 합격 여부: 불합격, 합격 확률:   0.01%
공부 시간:  0, 과외 시간:  1 합격 여부: 불합격, 합격 확률:   0.07%
공부 시간:  0, 과외 시간:  2 합격 여부: 불합격, 합격 확률:   0.32%
공부 시간:  0, 과외 시간:  3 합격 여부: 불합격, 합격 확률:   1.57%
공부 시간:  0, 과외 시간:  4 합격 여부: 불합격, 합격 확률:   7.28%
공부 시간:  0, 과외 시간:  5 합격 여부: 불합격, 합격 확률:  27.85%
공부 시간:  0, 과외 시간:  6 합격 여부:   합격, 합격 확률:  65.48%
공부 시간:  0, 과외 시간:  7 합격 여부:   합격, 합격 확률:  90.31%
공부 시간:  0, 과외 시간:  8 합격 여부:   합격, 합격 확률:  97.86%
공부 시간:  0, 과외 시간:  9 합격 여부:   합격, 합격 확률:  99.56%
공부 시간:  0, 과외 시간: 10 합격 여부:   합격, 합격 확률:  99.91%