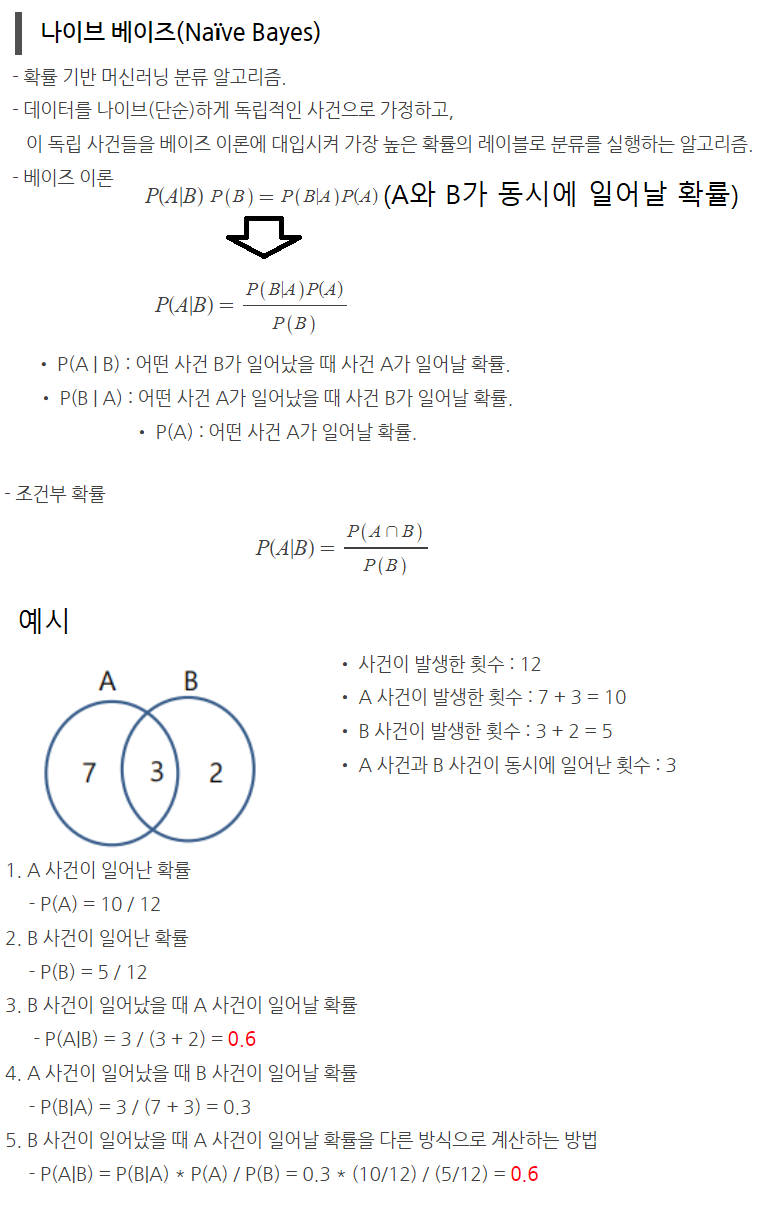
40_Gaussian_Naive_Bayes_가우시안나이브베이즈

import warnings
warnings.filterwarnings('ignore')
import numpy as np
import pandas as pd
import sklearn

가우시안 나이브 베이즈를 활용한 붓꽃 분류
iris 데이터를 활용해 데이터의 특징에 따라 붓꽃의 종류를 구분한다.

# 사이킷런에서 제공하는 iris 데이터를 불러오기 위해서 import 한다.
from sklearn.datasets import load_iris
# 학습 데이터와 테스트 데이터를 손쉽게 나눌 수 있도록 import 한다.
from sklearn.model_selection import train_test_split
# 가우시안 나이브 베이즈로 iris 데이터를 분류하기 위해 import 한다.
from sklearn.naive_bayes import GaussianNB
# 분류 성능을 측정하기 위해 사이킷런의 metrics 모듈의 accuracy_score, classification_report를 import 한다.
from sklearn.metrics import classification_report
from sklearn.metrics import accuracy_score

# iris 데이터 셋을 불러온다.
dataset = load_iris()
# print(type(dataset)) # sklearn.utils.Bunch
# print(dataset.feature_names) # 열 이름
# 'sepal length (cm)' => 꽃 받침 길이, 'sepal width (cm)' => 꽃 받침 너비, 'petal length (cm)' => 꽃잎 길이, 
# 'petal width (cm)' => 꽃잎 너비
# print(dataset.data) # 데이터
df = pd.DataFrame(dataset.data, columns=dataset.feature_names)
# print(dataset.target) # 실제값, 0 => 'setosa', 1 => 'versicolor', 2 => 'virginica'
df['target'] = dataset.target
df.target = df.target.map({0: 'setosa', 1: 'versicolor', 2: 'virginica'})
# print(type(df))
df

	sepal length (cm)	sepal width (cm)	petal length (cm)	petal width (cm)	target
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa
2	4.7	3.2	1.3	0.2	setosa
3	4.6	3.1	1.5	0.2	setosa
4	5.0	3.6	1.4	0.2	setosa
...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	virginica
146	6.3	2.5	5.0	1.9	virginica
147	6.5	3.0	5.2	2.0	virginica
148	6.2	3.4	5.4	2.3	virginica
149	5.9	3.0	5.1	1.8	virginica

150 rows × 5 columns

데이터 시각화

setosa_df = df[df.target == 'setosa']
versicolor_df = df[df.target == 'versicolor']
virginica_df = df[df.target == 'virginica']

꽃 받침 길이

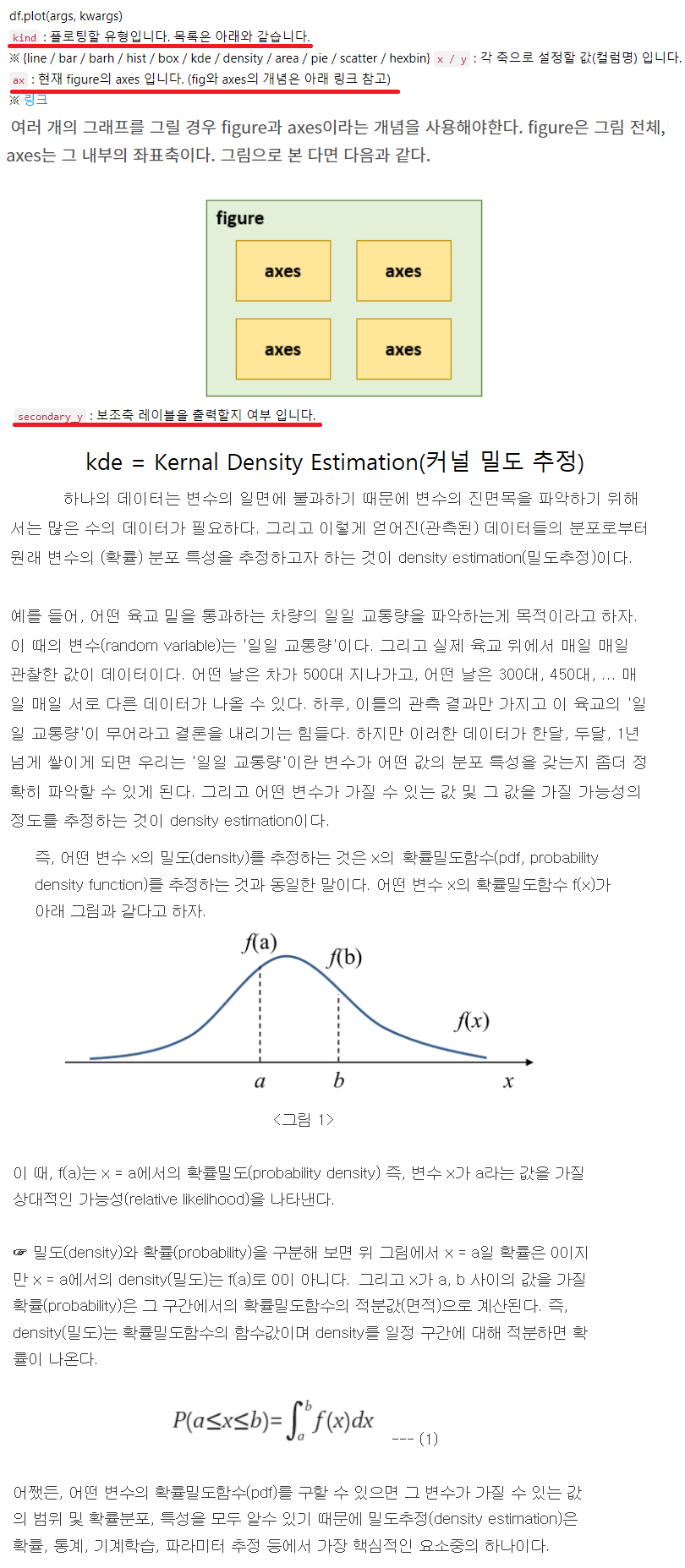
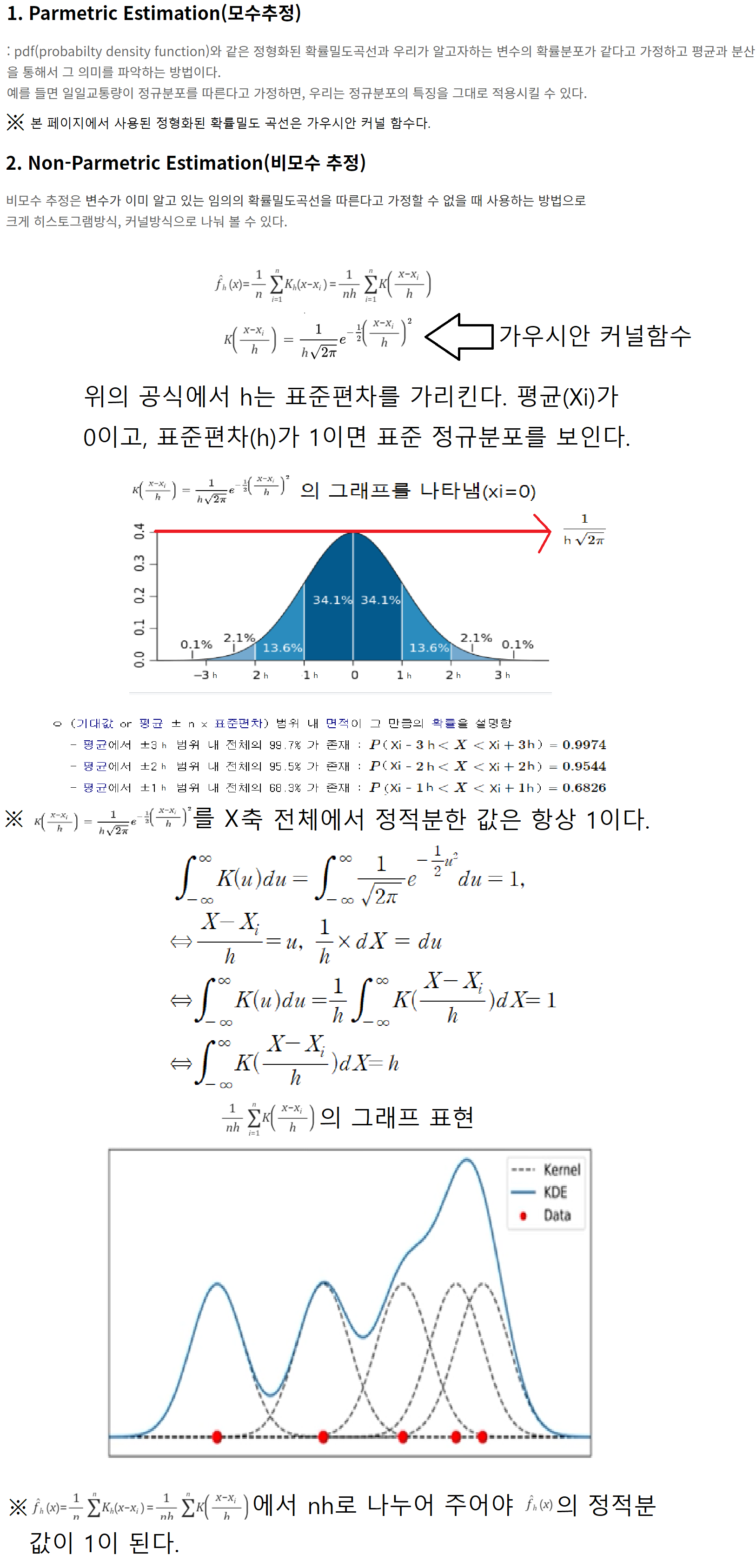
#https://wikidocs.net/159927
#https://darkpgmr.tistory.com/147
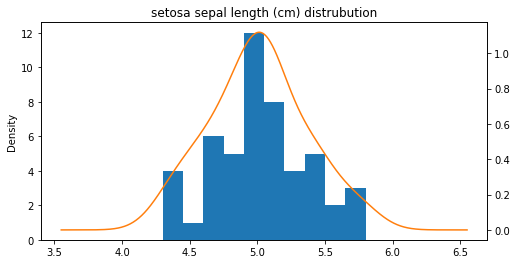
ax = setosa_df['sepal length (cm)'].plot(kind='hist')
setosa_df['sepal length (cm)'].plot(kind='kde', ax=ax, secondary_y=True, title='setosa sepal length (cm) distrubution', 
                                    figsize=[8, 4])

<AxesSubplot:label='7c4da28c-cf85-45da-b77a-4f85ad551c0f'>

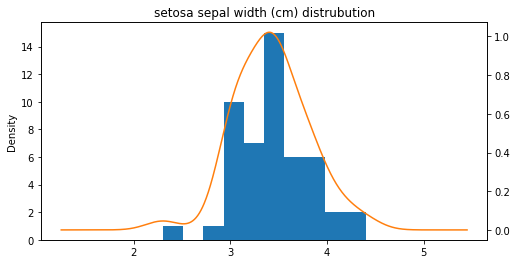
꽃 받침 너비

ax = setosa_df['sepal width (cm)'].plot(kind='hist')
setosa_df['sepal width (cm)'].plot(kind='kde', ax=ax, secondary_y=True, title='setosa sepal width (cm) distrubution', 
                                    figsize=[8, 4])

<AxesSubplot:label='532e2c24-4336-4397-9be1-f9994c383ba2'>

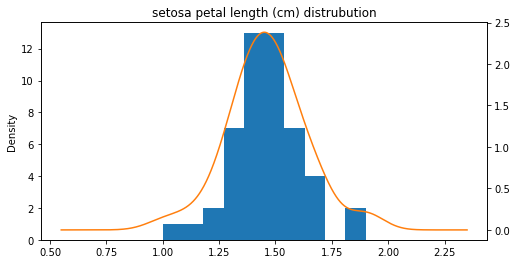
꽃잎 길이

ax = setosa_df['petal length (cm)'].plot(kind='hist')
setosa_df['petal length (cm)'].plot(kind='kde', ax=ax, secondary_y=True, title='setosa petal length (cm) distrubution', 
                                    figsize=[8, 4])

<AxesSubplot:label='e6906f89-fd8e-4653-8523-68bdc1ca5ba7'>

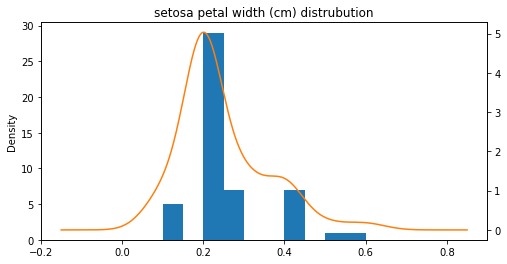
꽃잎 너비

ax = setosa_df['petal width (cm)'].plot(kind='hist')
setosa_df['petal width (cm)'].plot(kind='kde', ax=ax, secondary_y=True, title='setosa petal width (cm) distrubution', 
                                    figsize=[8, 4])

<AxesSubplot:label='814eba03-378b-41d4-876c-5f5ba9ad3e8b'>

데이터 다듬기

# 전체 데이터를 80%는 학습에 사용하고 나머지 20%는 테스트에 사용한다.
x_train, x_test, y_train, y_test = train_test_split(dataset.data, dataset.target, train_size=0.8, test_size=0.2)
print('x_train: {}, x_test: {}'.format(len(x_train), len(x_test)))
print('y_train: {}, y_test: {}'.format(len(y_train), len(y_test)))
print('꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비(문제): {}, 품종(답): {}'.format(x_train[0], y_train[0]))

x_train: 120, x_test: 30
y_train: 120, y_test: 30
꽃받침 길이, 꽃받침 너비, 꽃잎 길이, 꽃잎 너비(문제): [7.4 2.8 6.1 1.9], 품종(답): 2

가우시안 나이브 베이즈 모델 학습

model = GaussianNB()
model.fit(x_train, y_train)

GaussianNB()

테스트

predict = model.predict(x_test) # 학습 결과에 따른 테스트 데이터의 예측값을 계산한다.
print(classification_report(y_test, predict)) # 테스트 데이터의 실제값, 예측값
# accuracy: 정확도, precision: 정밀도, recall: 재현율, f1-score: f1 점수

              precision    recall  f1-score   support

           0       1.00      1.00      1.00        11
           1       0.91      1.00      0.95        10
           2       1.00      0.89      0.94         9

    accuracy                           0.97        30
   macro avg       0.97      0.96      0.96        30
weighted avg       0.97      0.97      0.97        30

print('정확도(accuracy): {}'.format(accuracy_score(y_test, predict))) # # 테스트 데이터의 실제값, 예측값

정확도(accuracy): 0.9666666666666667

comparsion = pd.DataFrame({'실제값': y_test, '예측값': predict})
comparsion

	실제값	예측값
0	0	0
1	1	1
2	0	0
3	0	0
4	2	2
5	1	1
6	2	2
7	2	2
8	0	0
9	0	0
10	0	0
11	1	1
12	0	0
13	1	1
14	1	1
15	2	1
16	1	1
17	1	1
18	2	2
19	2	2
20	1	1
21	0	0
22	0	0
23	2	2
24	1	1
25	2	2
26	0	0
27	0	0
28	2	2
29	1	1